Motion Blur All the Way Down

What happens if you take motion blur past its logical extreme? Here are some fun observations and ideas I encountered while trying to answer this question, with an attempt to apply the results in a procedural animation.

What is motion blur supposed to look like?

Motion blur started out purely as a film artifact, the result of a subject moving while the camera's shutter is open. This artifact turned out to be desirable, especially for videos, because it improves the perceptual similarity between a video and a natural scene, something I'll dive into in this section.

In a 3D and animation context, it's interesting to note that those two goals - looking natural, and simulating a camera, might not be in agreement, and might result in different motion blurs. I'll keep the simulation aspect as a side note, and ask what the most natural possible motion blur should look like. This can be broken down into a few questions:

Perception of motion in a natural scene

For the purpose of crafting motion blur, we can start by analyzing the very first steps of human vision, where the light hits our retina and phototransduction takes place. Under well-lit conditions, this is handled by cone-type cells. Phototransduction is not immediate, and we can model this lag by smoothing out the light stimulus over time.

Combining the above weighting function's shape with known human cone response times, we can create a detailed simulation of a perceived image based on any input scene. This concept has been used before, but without the shape of the time response.

/* Left: Example scene, assumed to be natural and continuous. Right: reconstructed perceived image. */ precision mediump float; #define PI 3.1415926535897932384626433832795 // Inputs varying vec2 iUV; uniform float iTime; uniform vec2 iRes; // These lines are parsed by dspnote to generate sliders uniform float time; //dspnote param: 0 - 0.1 (s) uniform float object_speed; //dspnote param: 0 - 40, 10 (rad/s) const float orbit = .2; const float uRad = .1; const float uniDensMul = 1.; vec3 diskColor = vec3(.8, .9, 1.); vec3 dashColor = vec3(1., .2, .2); vec3 vBarColor = vec3(.9, .9, .9); // the model weighting function is // W(x) = -a e^(-e^(a x + b) + a x + b) // with a=-50 and b=2.5 // integral of W from -inf to x: float weight_to_x(float x) { return exp(-exp(-50.*x+2.5)); } // integral of W from l to r: float weight_lr(float l, float r) { return weight_to_x(r) - weight_to_x(l); } // In polar coordinates, at radius posR, find the angle of the disk surface. // Returns 0 if posR is entirely outside the disk. // Returns -1 if posR is entirely inside the disk. float diskAngle(float posR, float diskR) { if (diskR <= 0.) return 0.; if (posR <= diskR-orbit) return -1.; float div = (orbit*orbit+posR*posR-diskR*diskR)/(2.*posR*orbit); if (abs(div) > 1.) return 0.; return acos(div); } float photoDisk(vec2 pol, float speed) { float da = diskAngle(pol.x, uRad); if (da == -1.) return 1.; // where does the disk occur in this pixel's past? // assuming: // - the current pixel is at 0 rad // - the disk currently covers 1 rad to 2 rad // - the disk is moving at 3 rad/sec // Then the disk was present from -1/3 sec to -2/3 sec. // Integrate the weighting function over this time interval. float ret = weight_lr(-(da-pol.y)/speed, -(-da-pol.y)/speed); return ret; } float dash(vec2 pol, float lol) { vec2 p = vec2(pol.x*cos(pol.y), pol.x*sin(pol.y)); p -= vec2(orbit, 0.); vec2 pol2 = vec2(length(p.xy), atan(p.y, p.x)-lol); float line = 1. - smoothstep(1., 2., abs(pol2.x - uRad)*iRes.y); line *= smoothstep(.05, .07, abs(mod(pol2.y/PI, .2)-.1)); return line; } void mainImage(inout vec4 fragColor, in vec2 fragCoord) { vec2 ratio = vec2(iRes.x/iRes.y, 1.); vec2 p = fragCoord/iRes.xy-0.5; vec2 p2 = ratio * vec2(mod(p.x, .5)-.25, p.y); p *= ratio; float speed = max(.001, object_speed); float rot = time*speed - PI + 1.; if (p.x < 0.) speed = 0.; vec2 pol = vec2(length(p2.xy), atan(p2.y, p2.x)); pol.y = mod(pol.y + rot, PI * 2.)-1.; vec3 col = vec3(0.); col = mix(col, diskColor, photoDisk(pol, max(.1, speed))); if (p.x > 0.) col = mix(col, dashColor, dash(pol, rot)); col = mix(col, vBarColor, 1. - smoothstep(3., 4., abs(p.x*iRes.x))); fragColor = vec4(col, 1.0); } void main(void) { vec4 color = vec4(0.0, 0.0, 0.0, 1.0); mainImage(color, gl_FragCoord.xy); gl_FragColor = color; }

[source] [full]

What this shows is that there already exists a natural blur at the photoreceptor level, a phenomenon often called motion smear. So why do we add artificial motion blur in videos, and what is the link between motion smear and motion blur?

Perception of a scene on a screen

Let's see what this perceived image looks like when viewing a screen with limited frames per second.

/* Left: Example scene, from a screen. Right: reconstructed perceived image. */ precision mediump float; #define PI 3.1415926535897932384626433832795 // Inputs varying vec2 iUV; uniform float iTime; uniform vec2 iRes; // These lines are parsed by dspnote to generate sliders uniform int video_motion_blur; //dspnote param: none | traditional | with_sine_shutter uniform float time; //dspnote param: 0 - 0.1 (s) uniform float object_speed; //dspnote param: 0 - 40, 10 (rad/s) const float orbit = .2; const float uRad = .1; const float uniDensMul = 1.; vec3 diskColor = vec3(.8, .9, 1.); vec3 dashColor = vec3(1., .2, .2); vec3 vBarColor = vec3(.9, .9, .9); void pR(inout vec2 p, float a) { p = cos(a)*p + sin(a)*vec2(p.y, -p.x); } // the model weighting function is // W(x) = -a e^(-e^(a x + b) + a x + b) // with a=-50 and b=2.5 // integral of W from -inf to x: float weight_to_x(float x) { return exp(-exp(-50.*x+2.5)); } // integral of W from l to r: float weight_lr(float l, float r) { return weight_to_x(r) - weight_to_x(l); } // the cosine shutter function is: // (1-cos((x-t1) 2 PI / (t2-t1)))/(t2-t1) if t1<x<t2 // 0 otherwise // this is the integral: float iCosShutter(float x, float t1, float t2) { if (x < t1) return 0.; if (x > t2) return 1.; float d = 1./(t2 - t1); x -= t1; return x*d - sin(2.*PI*x*d)/(2.*PI); } // In polar coordinates, at radius posR, find the angle of the disk surface. // Returns 0 if posR is entirely outside the disk. // Returns -1 if posR is entirely inside the disk. float diskAngle(float posR, float diskR) { if (diskR <= 0.) return 0.; if (posR <= diskR-orbit) return -1.; float div = (orbit*orbit+posR*posR-diskR*diskR)/(2.*posR*orbit); if (abs(div) > 1.) return 0.; return acos(div); } float photoDiskNoBlur(vec2 p, float diskA, float frameStart) { vec2 diskC = vec2(-orbit, 0.); pR(diskC, frameStart*object_speed); float amt = 1.-smoothstep(uRad, uRad+1./iRes.y, length(p - diskC)); // What time interval did this frame occur in? // Integrate the weighting function over this time interval. float ret = amt*weight_lr(time-frameStart, time-frameStart+1./60.); return ret; } float diskNoBlur(vec2 p, vec2 diskC, float frameN, float speed, bool screen) { float diskTot = 0.; if (screen) { diskTot = 1.-smoothstep(uRad, uRad+1./iRes.y, length(p - diskC)); } else { for (int i=0; i<10; i++) { float frame2N = frameN - float(i); float frame2Start = frame2N/60.; float diskA2 = frame2Start*speed; diskTot += photoDiskNoBlur(p, diskA2, frame2Start); } } return diskTot; } float screenDiskTrad(vec2 p, float frameStart, float speed) { vec2 pol = vec2(length(p.xy), atan(p.y, p.x)); pol.y = mod(pol.y + frameStart*speed, PI*2.)-PI; float da = diskAngle(pol.x, uRad); if (da == 0.) return 0.; if (da == -1.) return 1.; // Time intervals for shutter and object presence at this pixel. // Note the shutter interval should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -.5/60.; float shut2 = .5/60.; float obj1 = (pol.y-da)/speed; float obj2 = (pol.y+da)/speed; // the box shutter function is (shut1<t<shut2) ? 1/(shut2-shut1) : 0 // the object presence function is (obj1<t<obj2) ? 1 : 0 // find the integral of obj*shut // = definite integral of the shutter function from obj1 to obj2 float l = max(shut1, obj1); float r = min(shut2, obj2); return max(0., (r-l)/(shut2-shut1)); } float photoDiskTrad(vec2 p, float diskA, float frameStart) { vec2 diskC = vec2(-orbit, 0.); pR(diskC, frameStart*object_speed); float amt = screenDiskTrad(p, frameStart, max(.001, object_speed)); // What time interval did this frame occur in? // Integrate the weighting function over this time interval. float ret = amt*weight_lr(time-frameStart, time-frameStart+1./60.); return ret; } float diskTradBlur(vec2 p, vec2 diskC, float frameN, float speed, bool screen) { float diskTot = 0.; if (screen) { diskTot = screenDiskTrad(p, frameN/60., speed); } else { for (int i=0; i<10; i++) { float frame2N = frameN - float(i); float frame2Start = frame2N/60.; float diskA2 = frame2Start*speed; diskTot += photoDiskTrad(p, diskA2, frame2Start); } } return diskTot; } float screenDiskCos(vec2 p, float frameStart, float speed) { vec2 pol = vec2(length(p.xy), atan(p.y, p.x)); pol.y = mod(pol.y + frameStart*speed, PI*2.)-PI; float da = diskAngle(pol.x, uRad); if (da == 0.) return 0.; if (da == -1.) return 1.; // Time intervals for shutter and object presence at this pixel. // Note the shutter interval should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -1./60.; float shut2 = 1./60.; float obj1 = (pol.y-da)/speed; float obj2 = (pol.y+da)/speed; // integral of the shutter function from obj1 to obj2 return iCosShutter(obj2, shut1, shut2) - iCosShutter(obj1, shut1, shut2); } float photoDiskCos(vec2 p, float diskA, float frameStart) { vec2 diskC = vec2(-orbit, 0.); pR(diskC, frameStart*object_speed); float amt = screenDiskCos(p, frameStart, max(.001, object_speed)); // What time interval did this frame occur in? // Integrate the weighting function over this time interval. float ret = amt*weight_lr(time-frameStart, time-frameStart+1./60.); return ret; } float diskCosBlur(vec2 p, vec2 diskC, float frameN, float speed, bool screen) { float diskTot = 0.; if (screen) { diskTot = screenDiskCos(p, frameN/60., speed); } else { for (int i=0; i<10; i++) { float frame2N = frameN - float(i); float frame2Start = frame2N/60.; float diskA2 = frame2Start*speed; diskTot += photoDiskCos(p, diskA2, frame2Start); } } return diskTot; } float dash(vec2 p) { vec2 pol = vec2(length(p), atan(p.y, p.x)); float line = 1. - smoothstep(1., 2., abs(pol.x - uRad)*iRes.y); line *= smoothstep(.05, .07, abs(mod(pol.y/PI, .2)-.1)); return line; } void mainImage(inout vec4 fragColor, in vec2 fragCoord) { vec2 ratio = vec2(iRes.x/iRes.y, 1.); vec2 p = fragCoord/iRes.xy-0.5; vec2 p2 = ratio * vec2(mod(p.x, .5)-.25, p.y); p *= ratio; float speed = max(.001, object_speed); float frameN = floor(time*60.); float frameAge = fract(time*60.); float frameStart = frameN/60.; float diskA = frameStart*speed; vec2 diskC = vec2(-orbit, 0.); pR(diskC, frameStart*speed); float diskAmt = 0.; if (video_motion_blur == 0) { diskAmt = diskNoBlur(p2, diskC, frameN, speed, p.x < 0.); } else if (video_motion_blur == 1) { diskAmt = diskTradBlur(p2, diskC, frameN, speed, p.x < 0.); } else if (video_motion_blur == 2) { diskAmt = diskCosBlur(p2, diskC, frameN, speed, p.x < 0.); } vec3 col = vec3(0.); col = mix(col, diskColor, diskAmt); if (p.x > 0.) col = mix(col, dashColor, dash(p2 - diskC)); col = mix(col, vBarColor, 1. - smoothstep(3., 4., abs(p.x*iRes.x))); fragColor = vec4(col, 1.0); } void main(void) { vec4 color = vec4(0.0, 0.0, 0.0, 1.0); mainImage(color, gl_FragCoord.xy); gl_FragColor = color; }

[source] [full]

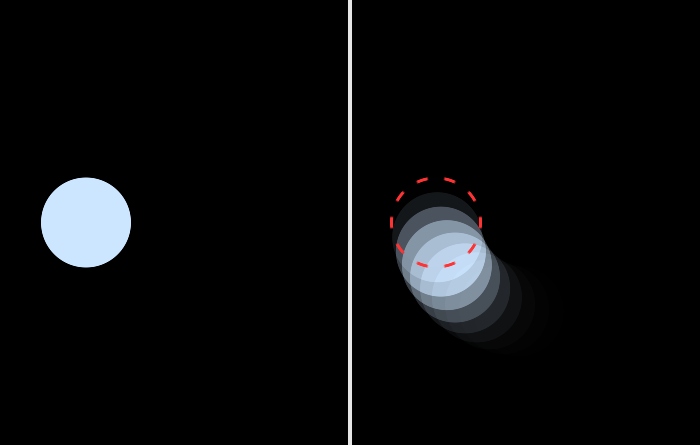
This finally gives us a way of visualizing the usefulness of motion blur. When viewing a video without motion blur, the resulting perceived image looks like overlaid frames instead of the expected motion smear. This situation is improved with a motion blurred video, where each frame no longer shows a moment in time, but an average of all the moments within the time interval covered by this frame. This is analogous to a video made with a camera whose shutter is open for the duration of each frame's timespan. The resulting perceived image looks a lot more similar to the natural case.

Making the screen natural with a shutter function

Something still looks off in the perceived image for traditional motion blur. At some object speeds, artifacts still appear as discontinuities in the motion smear. This can be almost eliminated by applying a shutter function: instead of averaging all the moments within a frame, we weight them by a function so that the start and end moments have less weight than the central moment of a frame. The name "shutter function" comes from the analogy to shutter efficiency in a diaphragm camera, where the shutter takes time to transition between open and closed states. But instead of simulating cameras, the shutter function can be chosen in a way that minimizes the perceptual difference between the screen and a natural scene. The problem then becomes very similar to crafting window functions in signal processing, and indeed the most popular window functions give very good results.

How well does this work? You can get a rough idea in the following demo, which can be switched between motion blur with and without a shutter function. My impression is that the shutter function is not necessary at low speeds, but is noticeably more natural for fast-moving objects¹. This makes it highly relevant to the "past the logical extreme" experiment I'm aiming for. It also looks smoother in still frames, which is incidental but sometimes relevant.

/* Left: Example scene, from a screen. Right: reconstructed perceived image. */ precision mediump float; #define PI 3.1415926535897932384626433832795 // Inputs varying vec2 iUV; uniform float iTime; uniform vec2 iRes; // These lines are parsed by dspnote to generate sliders uniform int video_motion_blur; //dspnote param: none | traditional | with_sine_shutter uniform float object_speed; //dspnote param: 0 - 40, 10 (rad/s) uniform float object_rot; //dspnote param const float orbit = .2; const float uRad = .1; const float uniDensMul = 1.; vec3 diskColor = vec3(.8, .9, 1.); vec3 gridColor = vec3(.2, .2, .5); void pR(inout vec2 p, float a) { p = cos(a)*p + sin(a)*vec2(p.y, -p.x); } // the cosine shutter function B is: // t1<x<t2: (1-cos(x-t1) 2 PI / (t2-t1))/(t2-t1) // otherwise 0 // this is the integral: float iCosShutter(float x, float t1, float t2) { if (x < t1) return 0.; if (x > t2) return 1.; float d = 1./(t2 - t1); x -= t1; return x*d - sin(2.*PI*x*d)/(2.*PI); } // In polar coordinates, at radius posR, find the angle of the disk surface. // Returns 0 if posR is entirely outside the disk. // Returns -1 if posR is entirely inside the disk. float diskAngle(float posR, float diskR) { if (diskR <= 0.) return 0.; if (posR <= diskR-orbit) return -1.; float div = (orbit*orbit+posR*posR-diskR*diskR)/(2.*posR*orbit); if (abs(div) > 1.) return 0.; return acos(div); } float screenDiskTrad(vec2 p, float frameStart, float speed) { vec2 pol = vec2(length(p.xy), atan(p.y, p.x)); pol.y = mod(pol.y + object_rot, PI*2.)-PI; float da = diskAngle(pol.x, uRad); if (da == 0.) return 0.; if (da == -1.) return 1.; // Time intervals for shutter and object presence at this pixel. // Note the shutter interval should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -.5/60.; float shut2 = .5/60.; float obj1 = (pol.y-da)/speed; float obj2 = (pol.y+da)/speed; // the box shutter function is (shut1<t<shut2) ? 1/(shut2-shut1) : 0 // the object presence function is (obj1<t<obj2) ? 1 : 0 // find the integral of obj*shut // = definite integral of the shutter function from obj1 to obj2 float l = max(shut1, obj1); float r = min(shut2, obj2); return max(0., (r-l)/(shut2-shut1)); } float screenDiskCos(vec2 p, float frameStart, float speed) { vec2 pol = vec2(length(p.xy), atan(p.y, p.x)); pol.y = mod(pol.y + object_rot, PI*2.)-PI; float da = diskAngle(pol.x, uRad); if (da == 0.) return 0.; if (da == -1.) return 1.; // Time intervals for shutter and object presence at this pixel. // Note the shutter interval should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -1./60.; float shut2 = 1./60.; float obj1 = (pol.y-da)/speed; float obj2 = (pol.y+da)/speed; // integral of the shutter function from obj1 to obj2 return iCosShutter(obj2, shut1, shut2) - iCosShutter(obj1, shut1, shut2); } void mainImage(inout vec4 fragColor, in vec2 fragCoord) { vec2 ratio = vec2(iRes.x/iRes.y, 1.); vec2 p = fragCoord/iRes.xy-0.5; p *= ratio; float speed = max(.001, object_speed); float frameN = floor(iTime*60.); float frameAge = fract(iTime*60.); float frameStart = frameN/60.; float diskA = object_rot; vec2 diskC = vec2(-orbit, 0.); pR(diskC, object_rot); float diskAmt = 0.; if (video_motion_blur == 0) { diskAmt = 1.-smoothstep(uRad, uRad+1./iRes.y, length(p - diskC)); } else if (video_motion_blur == 1) { diskAmt = screenDiskTrad(p, frameN/60., speed); } else if (video_motion_blur == 2) { diskAmt = screenDiskCos(p, frameN/60., speed); } vec2 gridP = abs(mod(p, .16) - vec2(.08)); float gridAmt = 1.-smoothstep(.6/iRes.x, 1.6/iRes.x, gridP.x); gridAmt = max(gridAmt, 1.-smoothstep(.6/iRes.y, 1.6/iRes.y, gridP.y)); vec3 col = vec3(0.); col = mix(col, gridColor, gridAmt); col = mix(col, diskColor, diskAmt); fragColor = vec4(col, 1.0); } void main(void) { vec4 color = vec4(0.0, 0.0, 0.0, 1.0); mainImage(color, gl_FragCoord.xy); gl_FragColor = color; } fig.onrender = () => { fig.params['object_rot'].value += fig.params['object_speed'].value * fig.timeDiff / 1000; if (fig.params['object_rot'].value > Math.PI*2) { fig.params['object_rot'].value -= Math.PI*2; } };

[source] [full]

I'll emphasize that this perceptual approach to motion blur is not conventional and could be misguided in some way. The common approach is to simulate cameras, which results in zero time overlap between frames, and often entirely discards moments that fall between frames. Meanwhile, the method I'm describing results in overlapping time-ranges for successive frames. With that out of the way, let's try applying this technique.

Getting irrational with the torusphere

To make things both difficult and interesting, I decided to make this infinite motion blur animation as a realtime shader. Because I like hardship and misery, yes, but mostly because I'd like the end product to be interactive, and in this case, a shader might be the simplest way.

First, how does one render motion blur in realtime? After ruling out multisampling² and analytic ray-traced motion blur³, I settled on a terrible hack best described as "integrated volume motion blur". Represent the moving object as a function that takes coordinates (including time) and returns density (the inside is 1, the rest is 0). Integrate this density function over time, and the result should give you a "motion-blurred density" over any time interval. The result can be rendered by volume ray casting. This method is not photorealistic, but can handle extremely long trails with realtime performance.

The intended animation combines an orbiting sphere and a rotating torus, both of which need to be motion-blurred up to essentially infinite speed.

Motion-blurred sphere

Taking a 2D slice of the orbiting sphere, the problem is reduced to finding the motion-blurred density for an orbiting circle. Let's assume an orbital radius $R$, and a circle of radius $a$. The circle's center is always at a distance of $R$ from the origin, so it can start at the point $(R, 0)$. This means that initially, all points $(x, y)$ on the circle are defined by:

$$ (x - R)^2 + y^2 = a^2 $$

In order to work with the orbit, this should be expressed in polar coordinates $(r,\theta)$, which can be done by substitution:

$$ r^2 - 2 r R \cos\theta + R^2 = a^2 $$

Finding the density function means taking any point, and answering the question: When does this point enter the orbiting circle? When does it exit? The answer lies in the angle coordinate coordinate $\theta$ of the initial object's surface, with the same radial coordinate $r$ as the given point. Because the object is orbiting, this angle is directly related to the time when the object will hit the point. So let's find $\theta$ based on the above definition of the surface:

$$ \theta = \pm\arccos\frac{R^2 + r^2 - a^2}{2 r R}, \theta\in[-\pi,\pi] $$

The $\pm$ sign comes from the inversion of $\cos$. This $\pm$ is useful, since it determines which half-circle is defined: positive or negative $\theta$. The two halves can be combined to get a polar expression of the density $\rho$ of the corresponding disk:

From this starting position, the disk is orbiting around the origin. This is equivalent to removing the time $t$ times the speed $v$ from the angle coordinate:

$$ \rho(\colorbox{yellow}{t,}r,\theta) = \begin{cases} 1 & \text{if }-h(r)\lt\theta\colorbox{yellow}{- v t}\lt h(r) \cr 0 & \text{otherwise} \end{cases} $$

We can separate $t$ from the time interval $I$ during which the object is present at a point $(r,\theta)$:

$$ \rho(t, r,\theta) = \begin{cases} 1 & \text{if }t\in I \cr 0 & \text{otherwise} \end{cases}\\[2ex] I=\left[\cfrac{\theta-h(r)}{v}, \cfrac{\theta+h(r)}{v}\right] $$

The motion-blurred density is the integral of the density $\rho$ over the current frame's time interval $F$. This works out to be the length of the intersection between $I$ and $F$. This can also be described intuitively: we're measuring how much of the frame's time is occupied by the object at a given point in space.

$$\int_F\rho(t,r,\theta) d t = \int_{F\cap I}1\ d t = |F\cap I|$$

Let's apply a shutter function $s$. For simplicity, assume $s$ is already centered on the current frame's time span. We can apply it by multiplying the density with $s(t)$ before integrating, replacing the need for any bounds of integration of the density. If $s$ has an antiderivative $S$, then the motion-blurred density becomes:

$$ \int\rho(t,r,\theta) s(t) d t = \int_I s(t) d t = S(\max I)-S(\min I) $$

This can be implemented in a shader and works with any shutter function, however, based on the goals from the first part of this article, shutter functions should have an integral of 1 and should overlap in such a way that the sum of all shutter functions at any timepoint is always 1. This can be satisfied with a trapezoid function, or with a sinusoid function such as this one, used in the animation:

$$ s(t)=\begin{cases} \cfrac{1-\cos\frac{(t-A)2\pi}{B-A}}{B-A} & \text{if }A\lt t\lt B \cr 0 & \text{otherwise} \end{cases}\\[2ex] A=\min F-\frac{|F|}{2},B=\max F+\frac{|F|}{2} $$

Motion-blurred torus

The same process can be followed for the torus. A 2D vertical slice of a torus is called a spiric section, or Spiric of Perseus. Aside from sounding like an epic videogame weapon, it also has a convenient formulation in polar coordinates. Take a torus of minor radius $a$ and major radius $b$. Take a section at position $c$, and within this section in polar coordinates $(r,\theta)$, all torus points are defined by:

$$ (r^2-a^2+b^2+c^2)^2 = 4b^2(r^2\cos^2\theta+c^2) $$

Solving for $\theta$, assuming $\theta\in[-\pi/2,\pi/2]$, this becomes:

$$ \theta = \pm\arccos\frac{\sqrt{(a^2 - b^2 - c^2 - r^2 - 2 b c) (a^2 - b^2 - c^2 - r^2 + 2 b c)}}{2 b r} $$

Once again, the inside of the torus is enclosed between the positive and negative cases of the $\pm$ sign, giving us a polar expression of the density of the solid torus. The remaining steps to get the motion-blurred rotating torus are exactly the same as for the sphere above.

/* Motion-blurred spiric section. */ precision mediump float; #define PI 3.1415926535897932384626433832795 // Inputs varying vec2 iUV; uniform float iTime; uniform vec2 iRes; // These lines are parsed by dspnote to generate sliders uniform int video_motion_blur; //dspnote param: traditional | with_sine_shutter uniform float minor_radius; //dspnote param: 0.01 - 0.5, 0.2 uniform float major_radius; //dspnote param: 0.01 - 0.5, 0.3 uniform float slice_position; //dspnote param: -1 - 1, 0.1 uniform float rotation_speed; //dspnote param: 0 - 300, 10 (rad/s) const float time = 0.; // torus minor and major radius, squared and combined vec2 tor, tor2; float torCst; // the cosine shutter function is: // (1-cos((x-t1) 2 PI / (t2-t1)))/(t2-t1) if t1<x<t2 // 0 otherwise // this is the integral: float iCosShutter(float x, float t1, float t2) { if (x < t1) return 0.; if (x > t2) return 1.; float d = 1./(t2 - t1); x -= t1; return x*d - sin(2.*PI*x*d)/(2.*PI); } // Within the slice at position z, in polar coordinates at radius r, // find the angle of the torus surface. // Returns 0 if r is entirely outside the torus. // Returns -1 if r is entirely inside the torus. float spiricPolarSurface(float r, float z) { float r2 = r*r; float z2 = z*z; float sum = torCst-2.*tor2.x*z2-2.*tor2.x*r2-2.*tor2.y*z2+2.*tor2.y*r2+z2*z2+2.*z2*r2+r2*r2; if (sum < 0.) return -1.; float sq = sqrt(sum)/(2.*tor.y*r); if (abs(sq) > 1.) return 0.; return acos(sq); } float tradMotionBlur(float obj1, float obj2) { // Shutter time interval. Should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -.5/60.; float shut2 = .5/60.; // the box shutter function is (shut1<t<shut2) ? 1/(shut2-shut1) : 0 // the object presence function is (obj1<t<obj2) ? 1 : 0 // find the integral of obj*shut // = definite integral of the shutter function from obj1 to obj2 float l = max(shut1, obj1); float r = min(shut2, obj2); return max(0., (r-l)/(shut2-shut1)); } float cosMotionBlur(float obj1, float obj2) { // Shutter time interval. Should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -.5/60.; float shut2 = .5/60.; // integral of the shutter function from obj1 to obj2 return iCosShutter(obj2, shut1, shut2) - iCosShutter(obj1, shut1, shut2); } float halfTorusDensity(vec2 pol, float z, float speed) { float da = spiricPolarSurface(pol.x, z); if (da == 0.) return 0.; if (da == -1.) return 1.; // Time interval for the object presence at this pixel. float obj1 = (pol.y-da)/speed; float obj2 = (pol.y+da)/speed; if (video_motion_blur==1) return cosMotionBlur(obj1, obj2); else return tradMotionBlur(obj1, obj2); } float torusDensity(vec3 p3d, float frameStart, float speed) { vec2 pol = vec2(length(p3d.xy), atan(p3d.y, p3d.x)); pol.y = mod(pol.y + frameStart*speed, PI*2.)-PI; float da = halfTorusDensity(pol, p3d.z, speed); pol.y = mod(pol.y + PI*2., PI*2.)-PI; float da2 = halfTorusDensity(pol, p3d.z, speed); if (da == 0. && da2 == 0.) return 0.; if (da == -1. || da2 == -1.) return 1.; return min(1., da+da2); } void mainImage(inout vec4 fragColor, in vec2 fragCoord) { vec2 ratio = vec2(iRes.x/iRes.y, 1.); vec2 p = fragCoord/iRes.xy-0.5; p *= ratio; tor = vec2(minor_radius, major_radius); tor2 = tor*tor; // precalculate constant for the spiric angle torCst = tor2.x*tor2.x + tor2.y*tor2.y - 2.*tor2.x*tor2.y; float frameN = floor(time*60.); float frameStart = frameN/60.; vec3 col = vec3(torusDensity(vec3(p, slice_position), frameStart, max(.001, rotation_speed))); fragColor = vec4(col, 1.0); } void main(void) { vec4 color = vec4(0.0, 0.0, 0.0, 1.0); mainImage(color, gl_FragCoord.xy); gl_FragColor = color; }

[source] [full]

Putting it together

All that's left is to "draw the rest of the owl" by combining elements in a convincing way, and by using standard volume ray casting on the result. Surface normals need extra care because there's no such thing as "motion-blurred surface normals", so they're just blended together here.

The animation should run below with basic mouse/touch interaction. It might not work well on all devices, so there's also a pre-rendered video at the top of the page. You can also find this shader on Shadertoy.

/* Infinite speed motion blur using volume ray casting. Blog post to go with it: https://www.osar.fr/notes/motionblur Also on Shadertoy: https://www.shadertoy.com/view/cdXSRn */ #extension GL_OES_standard_derivatives : enable precision mediump float; #define PI 3.14159265359 // Inputs varying vec2 iUV; uniform float iTime; uniform vec2 iRes; // These lines are parsed by dspnote for interaction uniform float cam_x; //dspnote param uniform float cam_y; //dspnote param // basic material, light and camera settings #define DIFFUSE .9 #define SPEC .9 #define REFLECT .05 const vec3 lightDir = normalize(vec3(-5, -6, -1)); #define CAM_D 2.4 #define CAM_H .75 // marching iterations #define ITER 40 #define SHADOW_ITER 20 // marching step, which depends on the size of the bounding sphere float stepSz; // torus shape ratio = minor radius / major radius #define TOR_RATIO .38 // speed for: time remapping; ball transition into orbit; object rotation #define TIMESCALE .015 #define RAD_SPEED 100. const float RT_RAD_SPEED = sqrt(RAD_SPEED); const float MAX_SPEED = floor(30./(TIMESCALE*PI*2.)+.5)*PI*2.; // remapped time for large scale events float T; // cycle duration in remapped time // it depends on the torus ratio because the radiuses zoom into each other const float C = log((1. + TOR_RATIO) / TOR_RATIO); const float D = C * .5; // ball and torus speed, rotation and transformation matrix float balSpeed, balRot, torSpeed, torRot; mat2 balMat, torMat; // ball and torus size and cycle progression float balSz, torSz, balCycle, torCycle; // ball and torus motion blur amplification float balAmp, torAmp; // torus minor and major radius, with squared version vec2 tor, tor2; // constants for torus angle and ball normals float torCst, balCst; // density and normity x-fades, ball orbit radius, cosmetic adjustments float densXf, normXf, balOrbit, torNormSz, strobe; // by Dave_Hoskins: https://www.shadertoy.com/view/4djSRW float hash14(vec4 p4) { p4 = fract(p4 * vec4(.1031, .1030, .0973, .1099)); p4 += dot(p4, p4.wzxy+33.33); return fract((p4.x + p4.y) * (p4.z + p4.w)); } // by iq: https://iquilezles.org/articles/filterableprocedurals/ float filteredGrid(vec2 p, float scale, vec2 dpdx, vec2 dpdy) { float iscale = 1./scale; float N = 60.0*scale; p *= iscale; vec2 w = max(abs(dpdx), abs(dpdy))*iscale; vec2 a = p + 0.5*w; vec2 b = p - 0.5*w; vec2 i = (floor(a)+min(fract(a)*N,1.0)- floor(b)-min(fract(b)*N,1.0))/(N*w); return (1.0-i.x*.6)*(1.0-i.y*.6); } // by iq: https://iquilezles.org/articles/smin/ float smin(float a, float b, float k) { float h = max(k-abs(a-b), 0.0)/k; return min(a, b) - h*h*k*(1.0/4.0); } mat2 rot2d(float a) { float c = cos(a); float s = sin(a); return mat2(c, -s, s, c); } // 2-point sphere intersection vec2 sphIntersect2(vec3 ro, vec3 rd, vec4 sph) { vec3 oc = ro - sph.xyz; float b = dot(oc, rd); float c = dot(oc, oc) - sph.w*sph.w; float h = b*b - c; if(h<0.0) return vec2(-1.0, -1.0); h = sqrt(h); return vec2(-b-h, -b+h); } // antiderivative of the cosine shutter function which is: // (1-cos((x-t1) 2 PI / (t2-t1)))/(t2-t1) if t1<x<t2 // 0 otherwise float iCosShutter(float x, float t1, float t2) { if (x < t1) return 0.; if (x > t2) return 1.; float d = 1./(t2 - t1); x -= t1; return x*d - sin(2.*PI*x*d)/(2.*PI); } // motion blurred density = integral of { object presence * window function } float cosMotionBlur(float obj1, float obj2) { // Shutter time interval. Should include the frameStart, but it's // moved to the pixel coordinates for easier wrap management. float shut1 = -1./60.; float shut2 = 1./60.; // integral of the shutter function from obj1 to obj2 return iCosShutter(obj2, shut1, shut2) - iCosShutter(obj1, shut1, shut2); } // Take a slice at depth y. In polar coordinates, at radius r, // find the polar angle of the ball surface. // Returns 0 if r is entirely outside the ball. // Returns -1 if r is entirely inside the ball. float ballPolarSurface(float r, float y) { float rad = balSz*balSz - y*y; if (rad <= 0.) return 0.; rad = sqrt(rad); if (r <= rad-balOrbit) return -1.; float div = (balOrbit*balOrbit+r*r-rad*rad)/(2.*r*balOrbit); if (abs(div) > 1.) return 0.; return acos(div); } // motion-blurred ball density float ballDensity(vec3 p, float speed) { p.xz *= balMat; p.z = abs(p.z); vec2 pol = vec2(length(p.xz), atan(p.z, p.x)); float bA = ballPolarSurface(pol.x, p.y); if (bA == -1.) return 1.; // Time interval for the object presence at this pixel. float obj1 = (pol.y-bA)/speed; float obj2 = (pol.y+bA)/speed; return cosMotionBlur(obj1, obj2); } // ball "normity", pseudo distance field to calculate normals float ballNormity(vec3 p) { p.xz *= balMat; p.z = abs(p.z); vec2 pol = vec2(length(p.xz), atan(p.z, p.x)); pol.y = max(0., pol.y-balCst); p.x = pol.x*cos(pol.y); p.z = pol.x*sin(pol.y); return length(p-vec3(balOrbit, 0., 0.))-balSz; } // Take a slice at depth z. In polar coordinates, at radius r, // find the polar angle of the torus surface. // Returns 0 if r is entirely outside the torus. // Returns -1 if r is entirely inside the torus. float spiricPolarSurface(float r, float z) { float r2 = r*r; float z2 = z*z; float sum = torCst-2.*tor2.x*z2-2.*tor2.x*r2-2.*tor2.y*z2+2.*tor2.y*r2+z2*z2+2.*z2*r2+r2*r2; if (sum < 0.) return -1.; float sq = sqrt(sum)/(2.*tor.y*r); if (abs(sq) > 1.) return 0.; return acos(sq); } // motion-blurred density of a half torus (a macaroni) float halfTorusDensity(vec2 pol, float z, float speed) { float da = spiricPolarSurface(pol.x, z); if (da == 0.) return 0.; if (da == -1.) return 1.; // Time interval for the object presence at this pixel. float obj1 = (pol.y-da)/speed; float obj2 = (pol.y+da)/speed; return cosMotionBlur(obj1, obj2); } // motion-blurred torus density float torusDensity(vec3 p3d, float speed) { p3d.xy *= torMat; vec2 pol = vec2(length(p3d.xy), atan(p3d.y, p3d.x)); pol.y = mod(pol.y, PI*2.)-PI; float da = halfTorusDensity(pol, p3d.z, speed); pol.y = mod(pol.y + PI*2., PI*2.)-PI; float da2 = halfTorusDensity(pol, p3d.z, speed); if (da == 0. && da2 == 0.) return 0.; if (da == -1. || da2 == -1.) return 1.; return min(1., da+da2); } // torus "normity", pseudo distance field to calculate normals float torusNormity(vec3 p, float speed) { p.xy *= torMat; float shell = abs(length(p)-tor.y)-tor.x*.3; vec2 q = vec2(length(p.xz)-tor.y,p.y); float torus = length(q)-tor.x; return -smin(speed*.002-torus, .1-shell, 0.1); } // combined density and normity float density(vec3 p) { float ball = ballDensity(p, balSpeed)*balAmp; float torus = torusDensity(p, torSpeed)*torAmp; return mix(ball, torus, densXf); } float normity(vec3 p) { return mix( ballNormity(p), torusNormity(p*torNormSz, torSpeed*.5), normXf); } vec3 getNormal(vec3 p) { float d = normity(p); vec2 e = vec2(.001, 0); vec3 n = d - vec3( normity(p-e.xyy), normity(p-e.yxy), normity(p-e.yyx)); return normalize(n); } // Because we're raycasting translucent stuff, this is called up to 28x per px // so let's keep it short vec3 material(vec3 normal, vec3 rayDir) { float diff = max(dot(normal, -lightDir), .05); vec3 reflectDir = -lightDir - 2.*normal * dot(-lightDir, normal); float spec = max(dot(rayDir, reflectDir), 0.); return vec3(.8,.9,1.) * (diff * DIFFUSE + spec * REFLECT); } // render torusphere by volume raycasting vec4 march(vec3 ro, vec3 rd, float marchPos, float marchBack) { float totMul = strobe*stepSz/0.05; vec4 col = vec4(0.); marchPos -= stepSz * hash14(vec4(rd*4000., iTime*100.)); int nMats = 0; for(int i=0; i<ITER; i++) { vec3 pos = ro + rd * marchPos; float d = clamp(density(pos)*totMul, 0., 1.); if(d > .002) { d = d*d*.5; float a2 = (1.-col.a)*d; vec3 n = getNormal(pos); col += vec4(material(n, rd)*a2, a2); if (col.a > 0.95) break; if (nMats++ > 28) break; } marchPos += stepSz; if (marchPos > marchBack) break; } if (col.a > 0.) col.rgb /= col.a; return col; } // render ground shadow by volume raycasting without material float shadowMarch(vec3 ro, vec3 rd, float marchPos, float marchBack) { float ret = 0.; float shadowStep = stepSz*2.; float totMul = .47*strobe*shadowStep/0.05; marchPos -= shadowStep * hash14(vec4(ro*4000., iTime*100.)); for(int i=0; i<SHADOW_ITER; i++) { vec3 pos = ro + rd * marchPos; float d = clamp(density(pos)*totMul, 0., 1.); if(d > .002) { d = d*d*.9; ret += (1.-ret)*d; if (ret > 0.95) break; } marchPos += shadowStep; if (marchPos > marchBack) break; } return min(1., ret); } // very inefficiently speed up the boring parts float retime(float t) { t *= TIMESCALE; float s = .5+1.7*t*PI*2./D; s = sin(s+sin(s+sin(s+sin(s)*0.3)*0.5)*0.75); return s*.06+t*1.7; } // ball<->torus crossfade used separately by density and normity float getXf(float x) { x = (abs(mod(x-(D/4.), C)-D)/D-.5)*2.+.5; // return smoothstep(0, 1, x) x = 2.*clamp(x, 0., 1.)-1.; return .5+x/(x*x+1.); } // The entire scene is necessarily zooming out. The ground texture deals with // that by crossfading different scales. const float GRID_CYCLE = log(64.); vec3 grid(vec2 pt, vec2 dx, vec2 dy, float phase, float t) { float freq = exp(-mod(t+GRID_CYCLE*phase, GRID_CYCLE))*7.; float amp = cos(PI*2.*phase+t*PI*2./GRID_CYCLE)*-.5+.5; float g = filteredGrid(pt, freq, dx, dy)*amp; return vec3(g,g,g); } void mainImage(inout vec4 fragColor, in vec2 fragCoord) { // set all the globals... T = retime(iTime+25.); // consider a modulo here balCycle = mod(T, C); torCycle = mod(T+D, C); // size of the bounding sphere for marching and step size float boundSz = exp(-min(torCycle, 5.*(C-mod(T-D, C)))); stepSz = boundSz/20.; // the ball/torus appear constant size and the camera appears to zoom out // in the code the camera distance is fixed and the objects are shrinking balSz = exp(-balCycle-D); torSz = exp(-torCycle); // the rotation is (theoretically) the integral of the speed, we need both balSpeed = .04*MAX_SPEED*(cos(T*PI*2./C)+1.); torSpeed = .04*MAX_SPEED*(cos((T+D)*PI*2./C)+1.); balRot = MAX_SPEED*(sin(T*PI*2./C)/(PI*2./C)+T)/C; torRot = MAX_SPEED*(sin((T+D)*PI*2./C)/(PI*2./C)+T)/C; if (balCycle<D) { balRot = MAX_SPEED*(floor(T/C+.5)*C+D)/C; balSpeed = 0.; } if (torCycle<D) { torRot = MAX_SPEED*(floor((T+D)/C+.5)*C)/C; torSpeed = 0.; } balMat = rot2d(balRot); torMat = rot2d(torRot); // torus minor and major radius and their squares tor = vec2(torSz/(1.+1./TOR_RATIO), torSz/(1.+TOR_RATIO)); tor2 = tor*tor; // precalculate constants for the spiric angle and ball normals torCst = tor2.x*tor2.x + tor2.y*tor2.y - 2.*tor2.x*tor2.y; balCst = 2.*balSpeed*smoothstep(30., 40., balSpeed); float bx = balCst*.037; balCst = (balCst+bx*bx*bx)*.004; // ball's orbital radius balOrbit = clamp(balCycle-D, 0., 2.*RT_RAD_SPEED/RAD_SPEED)-RT_RAD_SPEED/RAD_SPEED; balOrbit = .5+RT_RAD_SPEED*balOrbit/(balOrbit*balOrbit*RAD_SPEED+1.); balOrbit *= tor.y; // ball<->torus crossfade: the normity precedes the density slightly // this smoothens the max speed -> zero speed illusion densXf = getXf(T); normXf = getXf(T+0.06); // motion blur amplification is what makes this work balAmp = 1.+balSpeed*balSpeed*.00013; torAmp = 1.5+torSpeed*torSpeed*.00015; torNormSz = max(1., 8.*(torCycle-.76)); // Normalized pixel coordinates (from 0 to 1) vec2 uv = fragCoord/iRes.xy; // the strobe effect simulates overlap between fast spin and slow spin strobe = 1.-.1*(sin(iTime*83.+PI*smoothstep(.4, .6, uv.x))+1.)*(sin(2.2+T*PI*2./D)+1.)*.5; // camera float side = cos(CAM_H+cam_y)*CAM_D; float camT = iTime*0.05+PI*.75+cam_x; vec3 ro = vec3(sin(camT)*side, sin(CAM_H+cam_y)*CAM_D, cos(camT)*side); // camera position (ray origin) vec3 ta = vec3(0., 0., 0.); // camera target vec3 ww = normalize(ta - ro); vec3 uu = normalize(cross(ww,vec3(0.0,1.0,0.0))); vec3 vv = normalize(cross(uu,ww)); vec2 p = (-iRes.xy + 2.0*fragCoord)/iRes.y; vec3 rd = normalize(p.x*uu + p.y*vv + 2.*ww); // this starting color taints the entire scene (unintentional but why not) vec3 col = vec3(0.33, 0.18, 0.1); // the ground plane if (rd.y < 0.) { vec3 groundPt = ro + rd*(-(ro.y+.8) / rd.y); vec2 g2d = groundPt.xz; vec2 dx = dFdx(g2d); vec2 dy = dFdy(g2d); // the ground texture zooms out by crossfading different scales col += grid(g2d, dx, dy, 0., T)/3.; col += grid(g2d, dx, dy, 1./3., T)/3.; col += grid(g2d, dx, dy, 2./3., T)/3.; float sqDist = dot(g2d, g2d); col *= 2./(sqDist*.5*1.5+1.)-1.2/(sqDist*1.5*1.5+1.); // are we in the shadow of the bounding sphere? vec2 sphInter = sphIntersect2(groundPt, -lightDir, vec4(0.,0.,0.,boundSz)); if (sphInter != vec2(-1., -1.)) { // march the torusphere to draw the shadow float shad = shadowMarch(groundPt, -lightDir, sphInter.x, sphInter.y); col *= 1.-shad*.7; } } // the sky (only visible in interactive version) float up = dot(rd, vec3(0.,1.,0.)); col = mix(col, vec3(0.33, 0.18, 0.1)*.7, 1.-smoothstep(0., .02, abs(up)+.003)); col = mix(col, vec3(0.,0.,.1), smoothstep(0., .5, up)); // finally render the torusphere vec2 sphInter = sphIntersect2(ro, rd, vec4(0.,0.,0.,boundSz)); if (sphInter != vec2(-1., -1.)) { vec4 ts = march(ro, rd, sphInter.x, sphInter.y); col = mix(col, ts.rgb, ts.a); } fragColor = vec4(col, 1.); } void main(void) { vec4 color = vec4(0.0, 0.0, 0.0, 1.0); mainImage(color, gl_FragCoord.xy); gl_FragColor = color; } const tgt = fig.graphicsDiv; tgt.style.touchAction = 'none'; let startPointerX = -1, startCamX = 0; let startPointerY, startCamY = 0; tgt.onpointerdown = (ev) => { fig.activate(); tgt.setPointerCapture(ev.pointerId); startPointerX = ev.clientX; startPointerY = ev.clientY; startCamX = fig.params['cam_x'].value; startCamY = fig.params['cam_y'].value; }; tgt.onpointerup = (ev) => { tgt.releasePointerCapture(ev.pointerId); startPointerX = -1; }; tgt.onpointercancel = tgt.onpointerup; tgt.onpointermove = (ev) => { if (startPointerX === -1) return; fig.params['cam_x'].value = startCamX - 4*(ev.clientX - startPointerX)/tgt.clientWidth; fig.params['cam_y'].value = startCamY + 4*(ev.clientY - startPointerY)/tgt.clientHeight; if (fig.params['cam_y'].value > 0.75) fig.params['cam_y'].value = 0.75; if (fig.params['cam_y'].value < -1) fig.params['cam_y'].value = -1; fig.dirty = true; };

[source] [full]